Error
Skip to main content
Sorry, the requested file could not be found
More information about this error
Jump to… Jump to…ИНСТРУКЦИЯОбъявленияВариант 1Вариант 2Вариант 3РУССКИЙ ЯЗЫК Выпуск 1РУССКИЙ ЯЗЫК Выпуск 2РУССКИЙ ЯЗЫК Выпуск 3РУССКИЙ ЯЗЫК Выпуск 4РУССКИЙ ЯЗЫК Выпуск 5РУССКИЙ ЯЗЫК Выпуск 6РУССКИЙ ЯЗЫК Выпуск 7Русский язык выпуск 8РССКИЙ ЯЗЫК выпуск 9Вариант тестирования 1Вариант тестирования 2
Drop the block here to make it dock
Skip NavigationHome
Site pages
Courses
Факультет довузовской подготовки (ФДП)
Довузовская подготовка
Предуниверсариум
Наследники Бетанкура
Профориентация 2021
Математика ФДП
Обществознание (ФДП)
Русский язык (ФДП)
Физика ФДП
Факультет «Автоматизация и интеллектуальные технол.
 ..
..Факультет «Промышленное и гражданское строительство»
Факультет «Транспортное строительство»
- Факультет «Транспортные и энергетические системы»
Факультет «Управление перевозками и логистика»
Факультет «Экономика и менеджмент»
Факультет безотрывных форм обучения
Отдел аспирантуры
Институт непрерывного образования (ИНО)
Промышленный и городской транспорт (НОЦ ПГТ)
- Студенческое научное общество
Центр русского языка
Вопросы и ответы
Великолукский филиал ПГУПС
Ярославский филиал ПГУПС
Научно-образовательный центр инновационного развит.
 ..
..Центр целевой контрактной подготовки
Ученый совет Университета
- Открытый онлайн-курс «История транспорта»
Олимпиада «English for my future Profession»
Тестирование иностранных абитуриентов (Testing for.
 ..
..27.02.03 Диагностическая работа
Linear Equations Пошаговое решение математических задач
6.2 Решение линейных уравнений
Уравнения вида ax+b=0 называются линейными уравнениями относительно переменной x. В этом разделе мы будем заниматься проблемой решения линейных уравнений и уравнений, сводящихся к линейным уравнениям.
Мы определяем два уравнения как эквивалентные, если они имеют одно и то же множество решений. Следующие две операции над уравнением всегда приводят к новому уравнению, эквивалентному исходному. Этими операциями, иногда называемыми элементарными преобразованиями, являются:
T.1 Одно и то же выражение, представляющее действительное число, может быть добавлено к обеим частям уравнения.
T.2 Одно и то же выражение, представляющее ненулевое действительное число, может быть умножено на обе части уравнения.
Используя эти операции, мы можем преобразовать уравнение, множество решений которого неочевидно, через ряд эквивалентных уравнений в уравнение, имеющее очевидное множество решений.
Пример 1. Решить уравнение
(a) 2x-3=4+x
Добавьте -x к обеим сторонам, чтобы получить
-x+2x-3=-x+4+x (T.1)
или x-3=4
Добавьте 3 к обеим сторонам, чтобы получить
x-3+3=4+3 (T.1)
или x=7
Поскольку 2x-3=4+x эквивалентно x-3=4, что, в свою очередь, эквивалентно x=7, набор решений которого, очевидно, равен {7}, мы знаем, что набор решений (a) равен {7}.
Давайте посмотрим, как наш решатель линейных уравнений решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
Пример 2. Решите уравнение
Решите уравнение
(b) 1/2x+2/3=5/2x-1 1/2)x в обе стороны получить
2/3=5/2x-1/2x-1 (T.1)
или 2/3=2x-1
Добавить 1 к обеим сторонам, чтобы получить 9000 5
1+2/3=2x ( T.1)
или 5/3=2x
Умножьте обе части на 1/2, чтобы получить
5/6=x (T.2)
900 02 Таким образом, множество решений (b) равно {5/ 6}.Каждое линейное уравнение можно решить так же, как и в приведенных выше примерах. На самом деле, давайте рассмотрим общее линейное уравнение
х=-( б/а)
если а а!=0. Таким образом, общее линейное уравнение имеет в качестве решения множество {b/a}, если a!=0. Таким образом, каждое линейное уравнение имеет не более одного решения.
Следующие два примера представляют собой уравнения, которые сводятся к линейным уравнениям. 92 в обе стороны, чтобы получить
23+16y=9+30y
Теперь решим, как в предыдущих примерах.
23+16y=9+30y
23-9=30y-16y
14=14y
y=1
Таким образом, множество решений равно {1}.
Давайте посмотрим, как наш пошаговый математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
Пример 4. Решите уравнение
(c) (2x)/(x-1)=2/(x-1)+1
Замещающий набор (c) состоит из всех действительных чисел, кроме 1. Предполагая, что x!=1, мы умножаем оба стороны (c) на x-1, чтобы получить
(d) 2x=2+x-1,x!=1
Решая уравнение 2x =2+x- 1, мы получаем 1 как единственное решение Поскольку 1 не находится в замене (d), (d) не имеет решения. Кроме того, (c) эквивалентно (d), поэтому (c) не имеет решения.
6.3 Решение буквенных уравнений
Уравнение, содержащее более одной переменной или содержащее символы, представляющие константы, такие как a, b и c, может быть решено для одного из символов в терминах остальных символов с помощью применения операции T.1 и T.2 в предыдущем разделе. Студент столкнется с такими проблемами в других курсах.
Пример 1. Решите cx-3a=b для x.
Добавьте 3a с обеих сторон.
cx=b+3a
Умножьте обе части на 1/c.
x=(b+3a)/c
Последнее уравнение выражает x через другие символы.
Пример 2. Решите 3ay-2b=2cy для y.
Добавьте 2b с обеих сторон.
3ay=2cy+2b
Добавьте -2cy к обеим сторонам.
3ay-2cy=2b
Вычтите y.
(3a-2c)y=2b
Умножьте обе стороны на 1/((3A-2C))
Y = (2B)/(3A-2C)
Пример 3. Решение A/x+B/(2x) = C для x.
Умножьте обе стороны на 2x.
2a+b=2cx
2cx=2a+b
Умножить на 1/(2c).
x=(2a+b)/(2c)
В заключение этого раздела мы включим еще два примера, подобных тем, с которыми учащийся может столкнуться в других областях.
Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите похожую задачуВведите свою задачу
Пример 4. Решите A=P(1+rt) для r.
Применить распределительный закон.
A=P+Prt
Добавить -P к обеим сторонам.
A-P=Prt
Умножьте обе части на 1/(Pt).
(A-P)/(Pt)=r
Пример 5. Решить 1/R=1/r_1+1/r_2 для r_1.
Добавьте два члена справа.
1/(R)=(r_2+r_1)/(r_1r_2)
Умножить на Rr_1r_2.
r_1r_2=R(r_2+r_1)
r_1r_2=Rr_2+Rr_1
Добавить -Rr_1 к обеим сторонам.
r_1r_2-Rr_1=Rr_2
Вычтите r_1.
r_1(r_2-R)=Rr_2
Умножить на 1/(r_2-R).
r_1=(Rr_2)/(r_2-R)
6.4 Решение задач с формулировками
Одним из фундаментальных приложений алгебры является решение задач, сформулированных словами. Задача-постановка — это словесное описание ситуации, в которой участвуют как известные, так и неизвестные величины. В этом разделе каждая задача будет решена с помощью одного уравнения с одним неизвестным.
В этом разделе каждая задача будет решена с помощью одного уравнения с одним неизвестным.
Наша задача состоит в том, чтобы выбрать неизвестное и определить уравнение, которому оно должно удовлетворять. Хотя единого подхода ко всем проблемам не существует, иногда могут оказаться полезными следующие рекомендации:
1. Внимательно прочитайте задачу, пока полностью не поймете ситуацию.
2. Определите, какие количества запрашиваются, затем выберите то, которое лучше всего использовать в качестве неизвестного.
3. Установить связь между неизвестной и другими величинами в задаче.
4. Найдите информацию, которая говорит, какие две величины равны.
5. Используйте информацию в (4), чтобы написать уравнение.
6. Решите уравнение и проверьте решение, чтобы убедиться, что оно удовлетворяет исходной задаче.
На этом этапе основное внимание будет уделяться переводу задач-постановок в уравнения. Хотя некоторые задачи могут быть решены почти путем проверки, практика, которую мы приобретаем при составлении уравнений, окажется полезной при решении более сложных задач.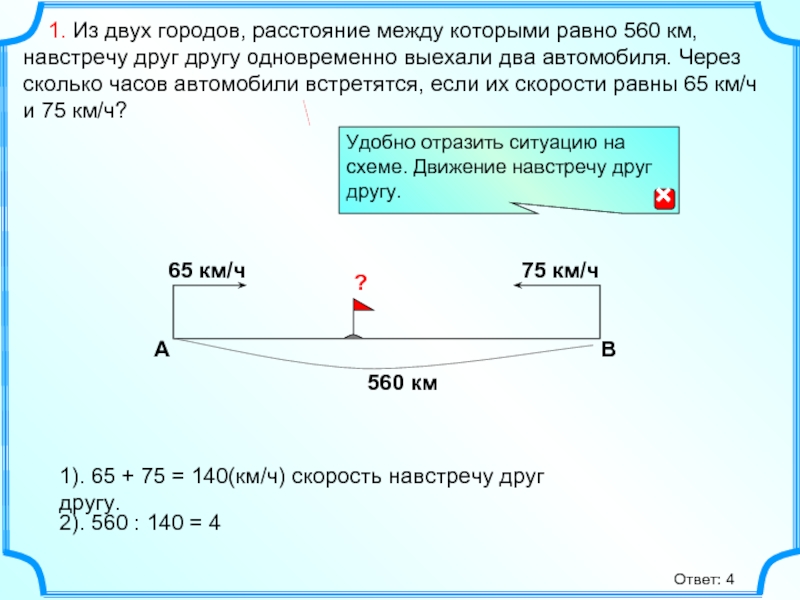
Пример 1. Если 2 раза прибавить определенное целое число к следующему последовательному целому числу, получится 34. Найдите целые числа.
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет первым целым числом.
Шаг 3. Тогда x+ 1 — следующее последовательное целое число.
Шаг 4. 2 раза определенное целое число плюс следующее последовательное целое число равно 34.
Шаг 5. 2x+(x+1)=34
Шаг 6. Решить.
2x+(x+1)=34
3x+1=34
3x=33
x=11
Проверить. 2*11+(11+1)=34
Пример 2. Боб и Джо вместе заработали 60 долларов. Оба получали одинаковую ставку, но Боб работал в три раза дольше, чем Джо. Сколько получил каждый?
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет количеством долларов, которые получил Джо.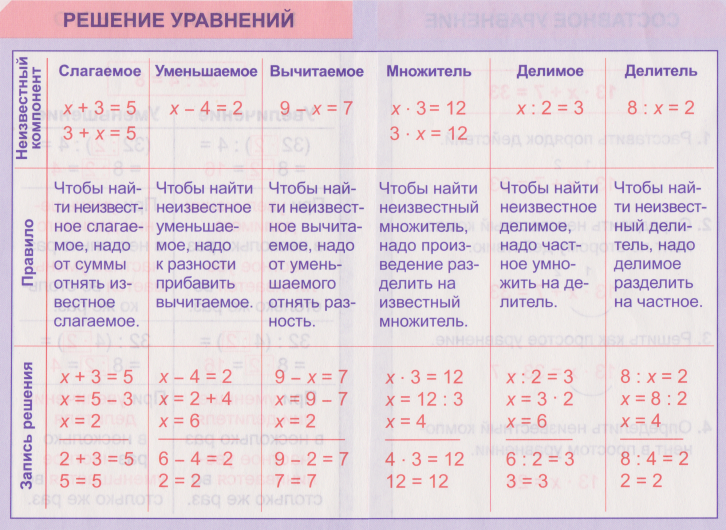
Шаг 3. Тогда умножьте на 3 количество долларов, которое получил Боб
Шаг 4. Боб и Джо вместе заработали 60 долларов.
Шаг 5. 3x+x=60
Шаг 6. Решить.
3x+x=60
4x=60
x=15
3x=45
Проверить 3*15+15=60
Пример 3. Сумма цифр двузначного числа равна 12. Если переставить цифры местами, число уменьшится на 36. Что это за число?
Шаг 1. Перечитайте!
Шаг 2. Пусть x — цифра десятков.
Шаг 3. Тогда 12 — x — это цифра единиц.
Шаг 4. Если цифры поменять местами, то число уменьшается на 36. Решать.
10(12-x)+x = 10x+ (12-x) -36
=120-10x+x=10x+12-x-36
=120-9x=9x-24 9000 5
=144= 18x
=x=8
=12-x=4
Поэтому число равно 84.
Проверьте. 84-36=48
84-36=48
Пример 4. Сколько фунтов конфет стоимостью 48 центов за фунт нужно добавить к 50 фунтам конфет стоимостью 80 центов за фунт, чтобы владелец магазина мог продавать конфеты по 60 центов за фунт ?
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет количеством фунтов конфет по 48 центов за фунт.
Шаг 3. Тогда 50+x будет фунтами конфет, которые он получит по 60 центов за фунт.
Шаг 4. Количество конфет по 48 центов за фунт, умноженное на 48 центов, плюс количество конфет по 80 центов за фунт, умноженное на 80 центов, должно быть равно количеству конфет по 60 центов за фунт, умноженному на 60 центов.
Шаг 5. (48 центов/фунт)(x фунтов) + (80 центов/фунт) (50 фунтов) = (60 центов/фунт) [(50+x)фунт]
Шаг 6. Решить.
48x+80*50=60(50+x)
48x+4000=3000+60x
1000=12x
x=( 83(1)/3) фунтов
Проверьте. (83+1/3)48+80*50=60(50+83+1/3)
(83+1/3)48+80*50=60(50+83+1/3)
Задачи, связанные со скоростями (или скоростями), будут использовать формулу
d=rt
где d — пройденное расстояние, r — скорость, t — время. При использовании формулы d и r должны быть выражены в одних и тех же единицах расстояния, а r и t должны быть выражены в одних и тех же единицах времени.
Пример 5. Группа студентов поехала на озеро в северном лесу ловить рыбу. Они преодолели 380 миль за 7 часов, из них 4 часа по асфальтированной дороге, а остальное время по грунтовой дороге. Если средняя скорость по грунтовой дороге была на 25 миль в час меньше средней скорости по шоссе, то найти для каждого участка пути среднюю скорость и пройденное расстояние.
Шаг 1 . Перечитай!
Шаг 2. Пусть x будет скоростью на грунтовой дороге.
Шаг 3. Тогда х+25 — это скорость на шоссе.
Шаг 4. Расстояние, пройденное по шоссе, плюс расстояние, пройденное по грунтовой дороге, равно 380 милям. Шаг 5
Шаг 5
Шаг 6. Решить.
(x+25)4+3x=380
4x+100+3x=380
7x=280
x=40 миль в час
x+25=65 миль в час
Проверить. (40+25)4+40*3=380
Рабочие задачи, связанные со скоростью выполнения, часто можно решить, сначала найдя дробную часть задачи, выполняемой каждым человеком или машиной за одну единицу времени, а затем найдя уравнение, которое связывает эти различные дробные части.
Пример 6. Мальчик может подстричь газон за 4 часа, а отец за 3 часа. Сколько времени им понадобится, чтобы подстричь один и тот же газон, работая вместе?
Шаг 1. Перечитайте!
Шаг 2. Пусть x будет количеством часов, которые им потребуется, чтобы подстричь газон Работая вместе.
Шаг 3 . Выберите один час в качестве нашей единицы времени. Теперь мальчик может скосить 1/4 газона за один час, отец может скосить 1/3 газона за один час, а вместе они могут скосить 1/x газона за один час.
Шаг 4. Сумма, срезанная мальчиком за один час, плюс сумма, срезанная отцом за один час, равна количеству, которое они могут срезать вместе за один час.
Шаг 5. 1/3+1/4=1/x
Шаг 6. Решить.
1/3+1/4=1/x
7/12=1/x
x=12/7 часов
Скорость, расстояние и время – средний уровень алгебры
Задачи расстояния, скорости и времени являются стандартным применением линейных уравнений. При решении этих задач используйте соотношение скорость (скорость или скорость) умножить на время равно расстояние .
[латекс]r\cdot t=d[/латекс]
Например, предположим, что человек должен был двигаться со скоростью 30 км/ч в течение 4 часов. Чтобы найти общее расстояние, умножьте скорость на время или (30 км/ч) (4 ч) = 120 км.
Проблемы, которые нужно решить здесь, будут иметь несколько шагов больше, чем описано выше. Поэтому, чтобы систематизировать информацию в задаче, используйте таблицу. Пример базовой структуры таблицы ниже:
Поэтому, чтобы систематизировать информацию в задаче, используйте таблицу. Пример базовой структуры таблицы ниже:
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
Третий столбец, расстояние, всегда заполняется путем перемножения столбцов скорости и времени. Если указано общее расстояние обоих людей или поездок, поместите эту информацию в столбец расстояния. Теперь используйте эту таблицу, чтобы настроить и решить следующие примеры.
Джоуи и Наташа начинают с одной точки и идут в противоположных направлениях. Джоуи идет на 2 км/ч быстрее, чем Наташа. Через 3 часа расстояние между ними 30 км. С какой скоростью шел каждый?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Наташа | [латекс]г[/латекс] | [латекс]\текст{3 ч}[/латекс] | [латекс]\текст{3 ч}(р)[/латекс] |
| Джои | [латекс]r + 2[/латекс] | [латекс]\текст{3 ч}[/латекс] | [латекс]\текст{3 ч}(г + 2)[/латекс] |
Расстояние, пройденное обоими, составляет 30 км. Следовательно, необходимо решить уравнение:
Следовательно, необходимо решить уравнение:
[латекс]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r} {6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ км/ч} \end{array}[/latex]
Это означает, что Наташа идет со скоростью 4 км/ч и Джоуи идет со скоростью 6 км/ч.
Ник и Хлоя покинули свой лагерь на каноэ и поплыли вниз по течению со средней скоростью 12 км/ч. Они развернулись и пошли обратно вверх по течению со средней скоростью 4 км/ч. Всего поездка заняла 1 час. Через сколько времени отдыхающие развернулись вниз по течению?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Вниз по течению | [латекс]\текст{12 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{12 км/ч} (т)[/латекс] |
| Восходящий поток | [латекс]\текст{4 км/ч}[/латекс] | [латекс](1 — т)[/латекс] | [латекс]\текст{4 км/ч} (1 — т)[/латекс] |
Расстояние, пройденное вниз по течению, равно расстоянию, которое они прошли вверх по течению. Следовательно, необходимо решить уравнение:
Следовательно, необходимо решить уравнение:
[латекс]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16} &=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]
Это означает, что туристы плыли вниз по течению 0,25 ч и 0,75 ч плыли обратно.
Терри выезжает из дома на велосипеде со скоростью 20 км/ч. Через 6 часов Салли уезжает на скутере, чтобы догнать его, двигаясь со скоростью 80 км/ч. Сколько времени ей понадобится, чтобы догнать его?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Терри | [латекс]\текст{20 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{20 км/ч}(т)[/латекс] |
| Салли | [латекс]\текст{80 км/ч}[/латекс] | [латекс](т — \текст{6 ч})[/латекс] | [латекс]\текст{80 км/ч}(т — \текст {6 ч})[/латекс] |
Расстояние, пройденное обоими, одинаково. Следовательно, необходимо решить уравнение:
Следовательно, необходимо решить уравнение:
[латекс]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{- 60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]
Это означает, что Терри находится в пути 8 часов, а Салли нужно всего 2 часа, чтобы поймать до него.
Во время 130-километровой поездки автомобиль двигался со средней скоростью 55 км/ч, а затем снизил скорость до 40 км/ч до конца пути. Поездка заняла 2,5 часа. Сколько времени автомобиль ехал со скоростью 40 км/ч?
| Кто или что | Ставка | Время | Расстояние |
|---|---|---|---|
| Пятьдесят пять | [латекс]\текст{55 км/ч}[/латекс] | [латекс]т[/латекс] | [латекс]\текст{55 км/ч}(т)[/латекс] |
| Сорок | [латекс]\текст{40 км/ч}[/латекс] | [латекс](\текст{2,5 ч}-т)[/латекс] | [латекс]\текст{40 км/ч}(\текст{2,5 ч}-т)[/латекс] |
Расстояние, пройденное обоими, составляет 30 км. Следовательно, необходимо решить уравнение:
Следовательно, необходимо решить уравнение:
[латекс]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&& \dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]
Это означает, что время, потраченное на движение со скоростью 40 км/ч, было 0,5 ч.
Задачи расстояния, времени и скорости имеют несколько вариаций, в которых неизвестные смешиваются между расстоянием, скоростью и временем. Как правило, они включают решение задачи, в которой общее пройденное расстояние используется для равного некоторому расстоянию, или задачи, в которой расстояния, пройденные обеими сторонами, одинаковы. Эти задачи на расстояние, скорость и время будут рассмотрены позже в этом учебнике, где для их решения требуются квадратичные решения.
Для вопросов с 1 по 8 найдите уравнения, необходимые для решения задач. Не решить.
- A находится в 60 км от B. Автомобиль в A отправляется в B со скоростью 20 км/ч в то же время, что автомобиль в B отправляется в A со скоростью 25 км/ч.
 Сколько времени пройдет, прежде чем автомобили встретятся?
Сколько времени пройдет, прежде чем автомобили встретятся? - Два автомобиля находятся на расстоянии 276 километров друг от друга и одновременно начинают двигаться навстречу друг другу. Они едут со скоростями, различающимися на 5 км/ч. Если они встретятся через 6 ч, найдите скорость каждого из них.
- Два поезда, отправившиеся с одной станции, движутся в противоположных направлениях. Они едут со скоростями 25 и 40 км/ч соответственно. Если они стартуют одновременно, как скоро расстояние между ними составит 195 километров?
- Два курьера на велосипедах, Джерри и Сьюзен, едут в противоположных направлениях. Если Джерри едет со скоростью 20 км/ч, то с какой скоростью должна ехать Сьюзен, если через 5 часов их разделяет 150 километров?
- Пассажирский и товарный поезд одновременно отправляются навстречу друг другу из двух точек, удаленных друг от друга на 300 километров. Если скорость пассажирского поезда превышает скорость товарного поезда на 15 км/ч и они встречаются через 4 часа, то какой должна быть скорость каждого из них?
- Два автомобиля двинулись в одно и то же время в противоположных направлениях из одной и той же точки.
 Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км?
Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км? - Мужчина, имея в своем распоряжении 10 часов, совершил экскурсию на велосипеде, выезжая со скоростью 10 км/ч и возвращаясь пешком со скоростью 3 км/ч. Найдите расстояние, которое он проехал.
- Человек идет со скоростью 4 км/ч. Какое расстояние он может пройти за город и вернуться обратно на тележке, движущейся со скоростью 20 км/ч, если он должен вернуться домой через 3 часа с момента старта?
Решите вопросы с 9 по 22.
- Мальчик уезжает из дома на автомобиле со скоростью 28 км/ч и возвращается пешком со скоростью 4 км/ч. Поездка туда и обратно занимает 2 часа. Как далеко он едет?
- Моторная лодка выходит из гавани и плывет со средней скоростью 15 км/ч к острову. Средняя скорость на обратном пути 10 км/ч. На каком расстоянии от гавани находился остров, если в общей сложности путешествие заняло 5 часов?
- Семья ехала на курорт со средней скоростью 30 км/ч, а затем возвращалась по той же дороге со средней скоростью 50 км/ч.
 Найдите расстояние до курорта, если общее время в пути составило 8 часов.
Найдите расстояние до курорта, если общее время в пути составило 8 часов. - В рамках летной подготовки пилот-курсант должен был долететь до аэропорта, а затем вернуться. Средняя скорость до аэропорта составила 90 км/ч, а средняя скорость обратно – 120 км/ч. Найдите расстояние между двумя аэропортами, если общее время полета составило 7 часов.
- Сэм начинает движение со скоростью 4 км/ч из лагеря на 2 часа раньше Сью, которая едет со скоростью 6 км/ч в том же направлении. Через сколько часов Сью догонит Сэма?
- Человек едет со скоростью 5 км/ч. Через 6 часов другой человек стартует с того же места, что и первый, со скоростью 8 км/ч. Когда второй человек догонит первого?
- Моторная лодка выходит из гавани и плывет со средней скоростью 8 км/ч к маленькому острову. Два часа спустя каютный катер выходит из той же гавани и движется со средней скоростью 16 км/ч к тому же острову. Через сколько часов после отплытия катер с каютами будет рядом с моторной лодкой?
- Бегун на длинные дистанции стартовал с дистанции со средней скоростью 6 км/ч.
 Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна?
Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна? - Два человека едут в противоположных направлениях со скоростью 20 и 30 км/ч в одно и то же время и из одного и того же места. Через сколько часов расстояние между ними будет 300 км?
- Два поезда отправляются в одно и то же время из одного и того же места и едут в противоположных направлениях. Если скорость одного из них на 6 км/ч больше, чем скорость другого, и через 4 часа расстояние между ними составляет 168 км, какова скорость каждого из них?
- Два велосипедиста стартовали из одной точки и едут в противоположных направлениях. Один велосипедист едет в два раза быстрее другого. Через три часа их разделяет 72 километра. Найдите скорость каждого велосипедиста.
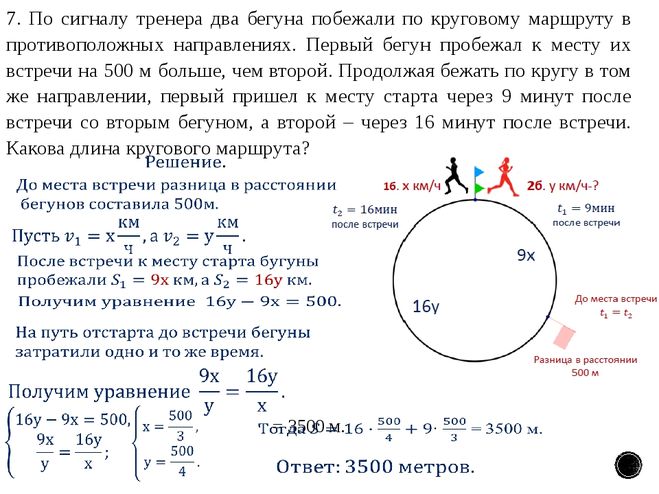
- Два маленьких самолета вылетают из одной точки и летят в противоположных направлениях. Первый самолет летит на 25 км/ч медленнее второго. Через два часа расстояние между самолетами составляет 430 километров.


 ..
.. ..
.. ..
.. Сколько времени пройдет, прежде чем автомобили встретятся?
Сколько времени пройдет, прежде чем автомобили встретятся? Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км?
Их скорости составляли 25 и 35 км/ч соответственно. Через сколько часов расстояние между ними составило 180 км? Найдите расстояние до курорта, если общее время в пути составило 8 часов.
Найдите расстояние до курорта, если общее время в пути составило 8 часов. Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна?
Через час второй бегун начал тот же маршрут со средней скоростью 8 км/ч. Через какое время после старта второго бегуна он догонит первого бегуна?