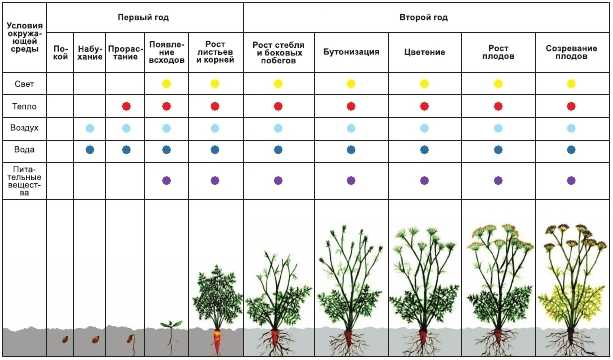
Сажаем плодовые деревья правильно

Свой плодовый сад – это не только частичка семейного очага, но часто и теплые детские воспоминания. В наш век современных технологий и химической промышленности это, прежде всего, источник полезных витаминов, минеральных веществ и природной энергии. Все мы понимаем, что «вечные, никогда не портящиеся» магазинные плоды наполнены пестицидами, удобрениями и покрыты химической пленкой для «вкусного» внешнего вида и сохранности. И от осознания этого факта наше желание иметь свои плодовые деревья с экологически чистым урожаем становится еще сильнее.

Но решение посадить даже одно плодовое дерево должно быть взвешенным. Любому растению в саду необходим уход, а за плодовыми и ягодными нужно «приглядывать» вдвойне, поскольку помимо пышного цветения, они будут вознаграждать вас вкусными и полезными плодами. Залог получения хороших и стабильных урожаев – это грамотная агротехника выращивания. Ошибки при посадке саженца могут проявиться только через несколько лет и быть непоправимыми, а драгоценное время будет упущено.

.. Поэтому мы рассмотрим с Вами основные нюансы, которые нужно предусмотреть при посадке плодовых деревьев.

Куда посадить?

Перед тем, как спланировать плодовый сад на своём участке, во-первых, обязательно определите близость залегания грунтовых вод к верхнему почвенному горизонту. Самый простой способ для этого – понаблюдать за уровнем воды в ближайшем колодце в разные периоды сезона. Второе, что надо определить, — не застаивается ли дождевая или талая вода. Как правило, она скапливается на тяжелых глинистых уплотненных почвах, где нет оттока воды за пределы участка. Все эти факторы вызывают почвенное переувлажнение, а нарушенный воздухообмен вызывает загнивание корней. Первым сигналом этому служит суховершинность — засыхание веток на верхушках деревьев.

Для успешного выращивания плодового сада грунтовые воды должны быть:

— для сильнорослых (семенных) подвоев не выше 3 м;

— для среднерослых (полукарликовых) — не выше 2,5 м;

— для слаборослых (карликовых) – не выше 1,5 м.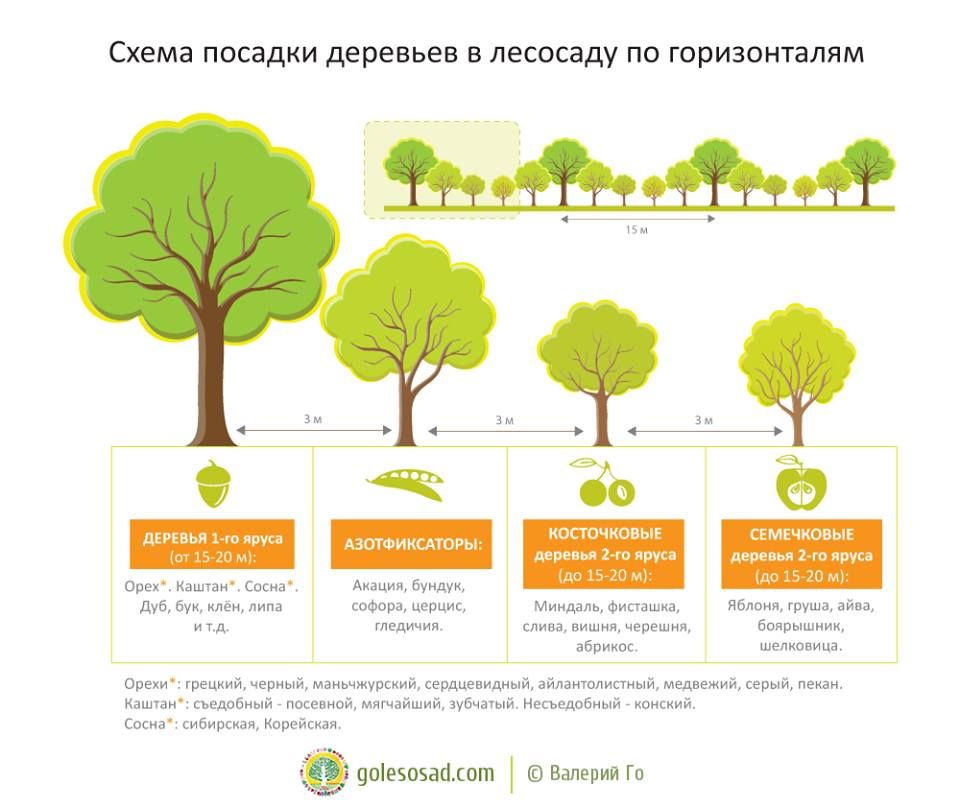

Если уровень грунтовых вод ближе 1 м, то вырастить плодовый сад, увы, не получится! Если вода от 1 до 1,5 м, то в этом случае применяется специальная технология высадки на холмиках (ее мы подробно рассмотрим в этой статье). При таком способе посадки корневая система находится выше уровня основного грунта, что значительно снижает риск ее вымокания.

Место посадки плодовых культур должно быть хорошо освещаемым, особенно в пик интенсивности фотосинтеза, то есть в утренние часы.

Саженцы сильнорослых плодовых деревьев на сильнорослых подвоях оптимально размещать на расстоянии 4-6 м друг от друга, среднерослых– 3-5 м, а низкорослых – 2-4 м.

Для создания плодового сада рекомендуем выбирать саженцы с закрытой корневой системой (выращенные в контейнере). Их можно высаживать с весны до осени, они легко приживаются, так как при пересадке их корневая система не травмируется, растение испытывает меньший стресс и быстрее акклиматизируется на новом месте.

Как же правильно посадить плодовые деревья с закрытой корневой системой?

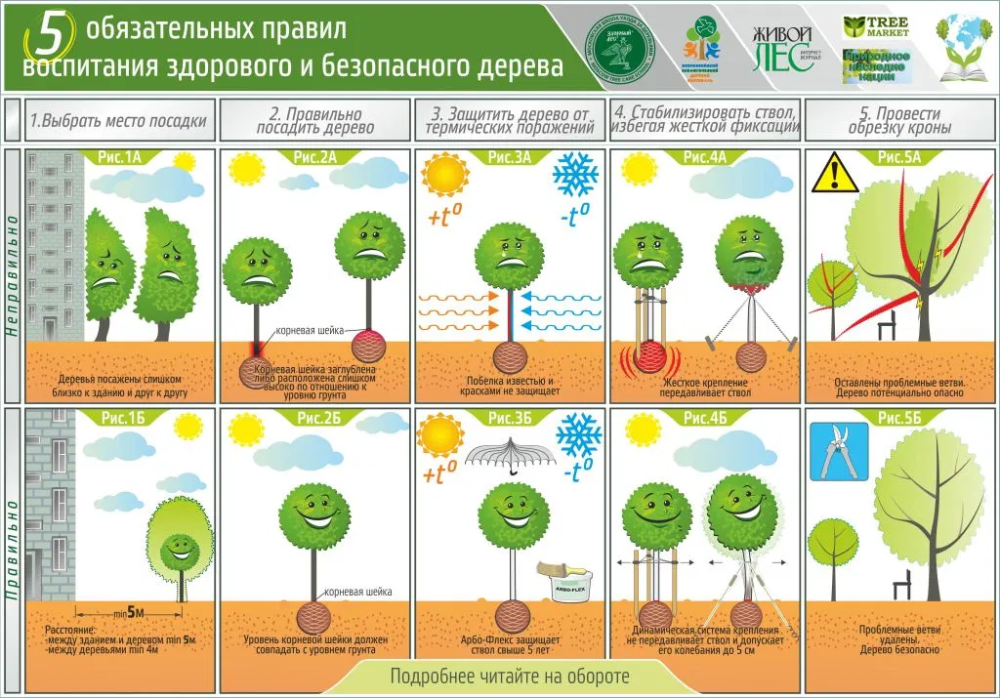
Самое важное при посадке плодовых деревьев – следить за положением корневой шейки, которая обязательно должна находиться над поверхностью грунта, ни в коем случае её нельзя заглублять! Правильное положение корневой шейки влияет на морозостойкость и дальнейшее развитие плодового дерева. Рассмотрим все этапы подробно:

1. ПОДГОТОВКА ПОСАДОЧНОЙ ЯМЫ.

Выкопайте посадочную яму глубиной 50—60 см и диаметром 0,8—1,2 м. Чем тяжелее почва, тем больше посадочная яма!

Именно до этой глубины в нашем климате располагается не менее 90% корневой системы растения. Ширина посадочной ямы может быть различной и определяется размером корневого кома растения. Для крупномеров с большим комом размер ямы увеличивают. Края ямы старайтесь сделать пологими т.к. корни в первую очередь будут расти вширь, и максимальное их количество сосредоточится у поверхности почвы.

Дно посадочной ямы разрыхлите ломом или перекопайте на глубину 20-25 см. При выкопке посадочной ямы отделяйте дернину, а также верхний плодородный слой от нижележащего грунта. Корни многолетних сорняков удалите. Далее подготовьте почвенную смесь для заполнения ямы.

2. ЗАПОЛНЕНИЕ ПОСАДОЧНОЙ ЯМЫ ПЛОДОРОДНОЙ СМЕСЬЮ:

Для заполнения посадочный ямы изъятый при выкапывании плодородный слой, смешивают с перегноем или компостом, добавляя комплексные минеральные удобрения (по норме казанной на упаковке) и известь (если почва избыточно кислая). Также можно купить готовый почвогрунт. Все компоненты необходимо смешать и, слегка утрамбовывая, заполнить яму так, чтобы уровень земли в ней был на 10-20 см выше основного уровня почвы. Это необходимо, чтобы при оседании почвы корневая шейка саженца не оказалась заглублена. Учитывайте это при посадке в рыхлую почву, которая после полива непременно осядет.

3. ПОСАДКА.

В посадочной яме сделайте углубление, размер которого должен соответствовать параметрам контейнера, в котором рос саженец в питомнике. Углубление пролейте водой. Не нарушая целостности корневого кома, аккуратно извлеките саженец их контейнера. Для этого ёмкость тщательно полейте и дайте впитаться влаге в течение 10 минут (при необходимости отпустите контейнер с саженцем в ёмкость с водой большего размера). Далее поместите саженец в углубление, чтобы уровень кома был на 2-3 см выше или совпадал с уровнем почвы в посадочной яме. Заполните пустоты плодородным грунтом и плотно прижмите почву вокруг ствола ногой. При уплотнении подошву ставьте пяткой от ствола, чтобы не повредить корневую систему саженца.

4. ПОЛИВ.

Обильно пролейте саженец в несколько приёмов (1-2 ведра). При необходимости добавьте плодородный грунт и повторите его уплотнение.

5. ПОДВЯЗКА.

Колышек для подвязки устанавливаем рядом с комом в посадочной яме так, чтобы не повредить корни. Размещать его лучше с северо-западной стороны от ствола саженца, для защиты растения от солнечных ожогов.

6. ЗАДЕРЖАНИЕ ВЛАГИ. МУЛЬЧИРОВАНИЕ.

Из остатков вынутого грунта вокруг посаженного деревца выложите валик (контур). Он поможет поливной и дождевой воде впитываться, пока саженец приживается. Замульчируйте почву под саженцем сухим плодородным грунтом, перегноем, торфом или скошенной травой. Это будет способствовать сохранению влаги. Во избежание подопревания коры следите, чтобы мульча не прикасалась к стволу!

Посадка на холм.

Такая посадка применяется на участках с близким уровнем грунтовых вод и основана на том, что основная масса питающих корней сосредоточена в верхнем слое почвы (до 50 см). При таком способе посадки выбирайте особо зимостойкие и скороплодные сорта.

Диаметр холма может достигать – 2-3 м в диаметре и высоты 0,5-1 м (форма конуса). Диаметр можно увеличивать по мере роста дерева, а вот высоту нужно продумать заранее, так как в дальнейшем поднять его уже будет нельзя, т.

к. корневая шейка должна будет остаться не заглублённой. Помните, что изначально подготовленная высота холма может «осесть» и стать ниже вдвое уже в течение первых двух лет.

Холм из высокоплодородной почвы, смешанной с перегноем и компостом, насыпается прямо на поверхность почвы без предварительной выкопки посадочных ям. Но если почва на Вашем участке тяжелая глинистая, то сначала создайте дренаж, насыпав под холм речной крупнозернистый песок с гравием слоем 5-10 см. Если почва песчаная, то для удержания влаги уложите слой торфа с глиной. Плодородную почвенную смесь подготовьте традиционным способом, с перегноем и минеральными удобрениями.

Холмы лучше готовить заранее, в идеале осенью предыдущего года. Высаживать плодовые деревья на холм следует не позднее двух месяцев до наступления устойчивых заморозков. На зиму, для защиты корней от подмерзания замульчируйте холм компостом или торфом слоем до 10 см.

Саженцы подвяжите к 2-3 колышками, чтобы они меньше раскачивались ветром и быстрее приживались.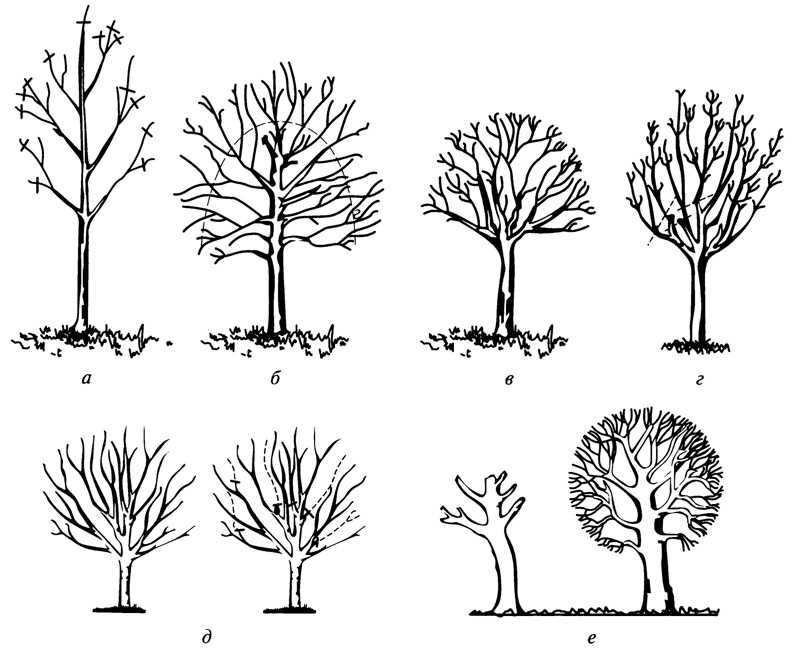 После посадки саженца по диаметру его кроны (около 1 м) сделайте земляные бортики шириной и высотой до 20 см, чтобы они удерживали воду и при этом не размывались.

Теперь наши деревья посажены, но это ещё не всё. Теперь они будут требовать Вашей постоянной заботы: полив, подкормки, защита от болезней и вредителей, а также регулярной обрезки для формирования кроны. А взамен подарят Вам свои вкусные и полезные плоды.

А самое важное, что нужно сделать перед тем как купить и посадить плодовые деревья — это выбрать нужные сорта и разобраться с подбором опылителей. В этом вопросе Вам снова помогут наши специалисты, справочные материалы и последующие статьи.

Тем садоводам, у кого уже есть свой плодовый сад, напоминаем, что в марте наступает пора весенней обрезки, с правилами которой мы предлагаем Вам ознакомиться в нашей статье «Семь раз отмерь — один раз отрежь!»

Больших Вам урожаев!

Совместимость деревьев в саду: что с чем сажать, чтобы урожай был хорошим

Вырастить ухоженный фруктовый сад, который будет давать богатые урожаи, очень непросто. Придется потратить много времени, сил и материальных затрат. Однако если не будет учтена совместимость деревьев и кустарников в саду при его закладке или пополнении коллекции растений, винить в неудаче придется только себя. Как избежать этой ошибки, вы можете узнать прямо сейчас.

Причины несовместимости садовых культур

Осваивая землю, садоводы-любители зачастую не утруждают себя составлением грамотного плана посадок. В лучшем случае, подбирают для определенной культуры участок с подходящей почвой и освещенностью, не учитывая, что соседствующие растения могут быть равнодушны друг к другу или даже враждовать. 

Основные факторы, приводящие к несовместимости растений друг с другом:

• расположение корней соседствующих культур в одном горизонте грунта, что приводит к конкурентной борьбе за влагу и питание;
• возникновение почвенной усталости в результате потребления одних и тех же питательных веществ из почвы;
• аллелопатия – выделение в воздух или почву веществ, угнетающих соседние растения, из-за чего нарушается их развитие, сдерживается плодоношение;
• затенение высокими деревьями низкорослых соседей, которые хиреют, не выдерживая конкуренции в борьбе за солнечный свет;
• наличие одинаковых заболеваний, вредителей.

Перед закладкой сада следует составить список растений, высадка которых планируется на участке. Разрабатывая схему посадок, обязательно нужно проверять, какие плодовые деревья можно сажать рядом друг с другом и с другими культурами. Оптимальная совместимость достигается, если сажать по соседству культуры одного вида, формируя, например, вишневый сад, яблоневый, грушевый и т. д. Но не многие могут это себе позволить, имея стандартный земельный участок. Поэтому в одной группе высаживают деревья со сходными условиями выращивания и отсутствием антагонизма.

На заметку. Используя добрососедство культур, можно повысить их урожайность. Посадив рядом растения-антагонисты, можно снизить или вовсе потерять урожай, а иногда и сами растения.

Конкуренция за выживаемость – как ее избежать

Культуры даже одного вида могут враждовать, вступая в борьбу за пространство, освещение, питание, и даже влагу, если посадки загущены. В таком случае угнетаются и погибают наиболее слабые экземпляры.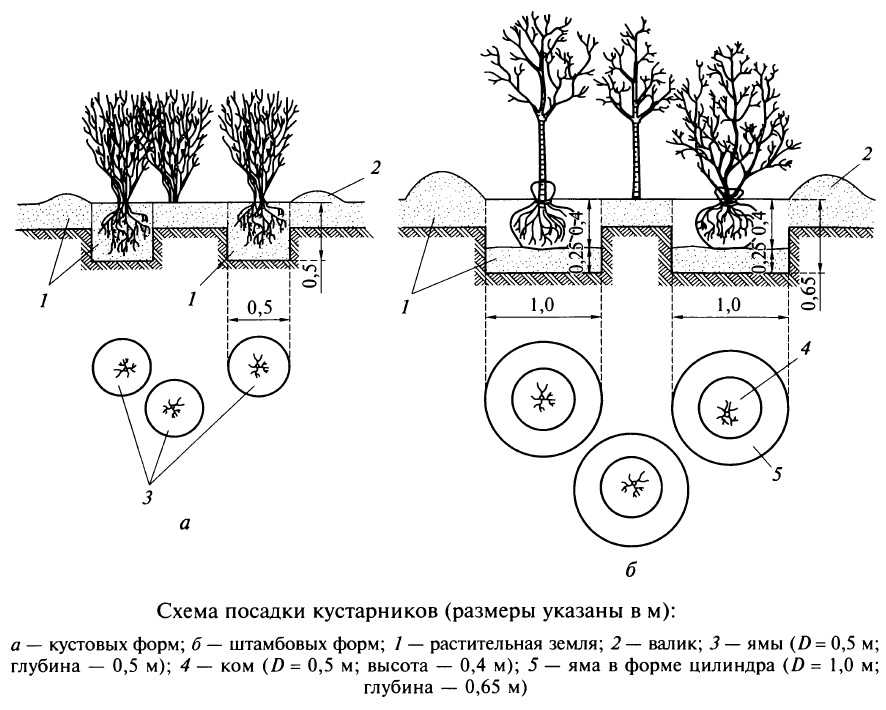 Чтобы этого не происходило, необходимо и в монопосадках удовлетворять требования каждой культуры к агротехнике, схеме посадки.

Пока саженцы малы, порой кажется, что расстояния между растениями при посадке, указанные в характеристиках, чрезмерны. Однако эти интервалы следует выдерживать, принимая во внимание размеры крон взрослых деревьев. Для каждой культуры они индивидуальны, а в среднем таковы:

• между совместимыми плодовыми культурами – 3 м;
• между растениями-конкурентами – минимум 5–7 м;
• между колоновидными  деревьями –2,5 м.

Если поблизости от садового участка лес, где растут такие деревья, как ясень, дуб, береза, нужно позаботиться, чтобы плодовые деревья располагались в семи, а лучше в десяти метрах от них. Находящиеся ближе дикоросы разросшимися корнями станут перехватывать влагу и питание у нежных культиваров.

Необходима пространственная изоляция и некоторых садовых кустарников: сирени, жасмина, барбариса, шиповника, калины, облепихи. Агрессивно разрастаясь, они подавляют развитие других культур, вытесняют их со «своей» территории.     

Совместимость садовых деревьев друг с другом и другими культурами

Здесь представлена информация о совместимости деревьев и кустарников в саду на примере самых распространенных на участках культур. Из плодовых растений наиболее популярны яблони, вишни, груши, сливы, в южных районах – еще абрикос, персик. Среди ягодных кустарников лидируют малина, смородина разных видов, крыжовник, виноград.

Яблоня

В совместных посадках яблоня, пока она молода, хорошо уживается с малиной. Более того, это культуры-компаньоны, благотворно влияющие друг на друга. Корни малины рыхлят землю, насыщают ее кислородом и обогащают азотом, листва при близком расположении способна защитить дерево от парши, а яблоня платит малине защитой от серой гнили. Но когда крона яблони разрастается, светолюбивой малине становится под ней некомфортно, и ягодные кусты приходится пересаживать.

Хороший сосед для этого растения клен ясенелистный: выделяемые им фитонциды уберегают яблоню от плодожорки. Крону клена ежегодно следует обрезать, оставляя максимум 1 м в высоту.

Культуры, рядом с которыми сажать яблоню не рекомендуется:

• вишня;
• грецкий орех;
• золотистая смородина;
• персик;
• рябина;
• тополь;
• черешня.

На заметку. Злейший антагонист яблони, который можно посадить только у противоположной стороны участка, – грецкий орех. Содержащийся в его листьях юглон является природным гербицидом и, накапливаясь в почве, уничтожает любую растительность. Но даже обычный картофель, посаженный в междурядьях, способен снизить урожай и ухудшить вкус яблок.

Груша

Не следует сажать грушу бок о бок с теми же растениями, что и яблоню. Исключение – тополь, особенно черный, для груши он приятный компаньон. Самый неблагоприятный ее сосед – можжевельник обыкновенный, поскольку на нем может развиваться и распространяться на другие растения ржавчина. Из ягодных кустарников самая нелюбимая соседка – золотистая смородина. Большинство сортов груш самобесплодны и нуждаются в компании других культиваров этого вида.

На заметку. Если яблоня готова принять грушу как желанную соседку, то груша, напротив, не любит находиться рядом с этим деревом, равно как и с косточковыми культурами.

Вишня

Прекрасно уживается вишня с черешней, виноградом и сливой. Нежелательно для нее соседство с грушами, некоторыми сортами яблонь, всеми видами смородины. Не следует, экономя посевную площадь, высаживать под вишнями землянику, перец, томаты. Нужно располагать подальше от вишен все пасленовые, которые могут заразить деревья вилтом (вертициллезным увяданием). В результате этого заболевания сердцевина побегов отмирает, и после цветения они усыхают.

На заметку. Не сажайте рядом с вишней красную рябину: вишне от этого плохо не будет, а рябина станет болеть, крона ее со стороны вишни оголится.

Слива

Сливе комфортно рядом с крыжовником, бузиной, кленом. Клен по соседству, если ему делать регулярную укорачивающую обрезку, стимулирует плодоношение сливы, черная бузина спасает от нашествия тли. Не конфликтует слива с яблоней, малиной, черной смородиной. Береза, фруктовые деревья (кроме яблони) – неподходящие соседи для этой культуры.

На заметку. Не допускайте смешанных посадок сортов маньчжурских разновидностей слив с западной (русской) сливой.

Виноград   

Хорошо себя чувствует виноград рядом с лимонником, розами, большинством косточковых и семечковых видов деревьев. Исключительно благоприятно соседство винограда с грушей. В некоторых садах можно видеть огромные грушевые деревья, в крону которых вплетаются лианы, увешанные солидными кистями солнечной ягоды. И дерево нисколько не страдает от этого.

Неблагоприятно для винограда близкое расположение клематисов, недопустимыми соседями для этой южной культуры являются айва и грецкий орех.

На заметку. Некоторые, казалось бы, безобидные огородные культуры, обедняя почву, способны замедлить рост виноградной лозы, снизить урожай ягод. К таким растениям относятся все пасленовые, подсолнечник.

Дополнительные сведения о том, какие соседи благоприятны для садовых культур, а какие недопустимы, можно почерпнуть из представленной ниже таблицы совместимости деревьев и кустарников в саду.

Таблица совместимости деревьев и кустарников в саду

Культура	Высокая совместимость	Низкая совместимость
Яблоня	Слива, малина	Вишня, черешня, золотистая смородина
Груша	Рябина, виноград	Вишня, слива, золотистая смородина
Виноград	Груша, яблоня, черешня, вишня
Вишня	Виноград, черешня, слива, яблоня	Груша, смородина
Слива	Яблоня, смородина, малина, крыжовник	Груша, вишня, черешня
Смородина черная	Яблоня	Слива, черешня, вишня, малина, красная смородина
Смородина красная	Крыжовник, вишня	Малина, смородина черная
Крыжовник	Вишня, красная смородина	Яблоня, малина, черная смородина
Малина	Яблоня	Крыжовник, смородина
Облепиха		Все культуры

Совместимость плодовых деревьев друг с другом и другими культурами учитывать стоит, но в определенной степени она условна. У некоторых грамотных садоводов уживаются на участке вроде бы абсолютно непримиримые виды растений. Правильная агротехника, регулярный уход за насаждениями способны нивелировать конкуренцию культур за выживаемость и привести к заслуженному успеху.

геометрия — посадить 9 деревьев в 10 рядов по 3

Я полностью переписал этот пост, надеюсь, он будет более последовательным.

Геометрическая головоломка предполагает родственную комбинаторную головоломку:

Для девяти объектов сколько существует неизоморфных наборов из десяти наборов по три объекта в каждом, таких, что никакие два набора не имеют более одного общего объекта?

Где две коллекции изоморфны, если существует перестановка 9 объектов (деревьев), которая преобразует одну коллекцию в другую.

Каждое решение геометрической головоломки дает решение комбинаторной. Таким образом, решения комбинаторной головоломки ограничивают возможности решения геометрической задачи и дают рекомендации по их нахождению.

Комбинаторная головоломка допускает только 4 решения:

Теорема: Ниже приведены единственные решения комбинаторной головоломки:

• Объекты: $\{A, B, C, 1, 2, 3, 4, 5 , 6\}$ Коллекции: $$ABC, A14, A25, A36, B15, B26, B34, C16, C24, C35$$ $$ABC, A14, A25, A36, B16, B24, B35, C13, C26, C45$$ $$AB1, AC2, BC3, A34, A56, B46, B25, C16, C45, 123$$
• Объекты: $\{A, B, C, D, 1, 2, 3, 4, *\}$ Коллекции: $$AB*, CD*, AC1, AD2, BC3, BD4, A34, B12, C24, D13$$

Доказательство:

Для такой коллекции определите экземпляр как множество $S$ в коллекции и дерево $t$ с $t\in S$. Так как существует $10$ наборов из $3$ деревьев каждый, всего $30$ экземпляров. Определите степень дерева как количество экземпляров, частью которого оно является. Дерево степени $n$ называется $n$-деревом. Так как есть 9 долларов$ деревья, средняя степень дерева $\frac {30}9 = 3\frac13$. Следовательно, некоторые деревья должны иметь степень $4$ или выше.

Лемма:

• Максимальная степень любого дерева $4$.
• Любое 4-дерево имеет общий набор со всеми остальными деревьями.
• Минимальная степень для любого дерева не менее половины числа 4-деревьев.

Доказательство:

Пусть $n$ степень дерева $T$. Тогда $n$ множеств, содержащих $T$, состоят из $2n$ экземпляров, отличных от $T$. Если любые два из этих экземпляров относятся к одному и тому же дереву, они не могут находиться в одном наборе, и поэтому два набора, в которых они находятся, имеют две общие точки (общую точку и $T$), что недопустимо. Таким образом, у нас должно быть $2n + 1$ различных деревьев (включая $T$). Итак, $2n + 1\le 9$ и $n \le 4$. Если $n = 4$, то представлены все деревья, поэтому 4-дерево делит набор со всеми остальными деревьями. Теперь для любого дерева $T$ оно должно иметь общий набор с каждым 4-деревом, поэтому количество 4-деревьев $d_4$ удовлетворяет $d_4 \le 2n$, или $n \ge \frac{d_4}2$

QED

Пусть $d_n$ — количество деревьев степени $n$. По лемме $n \le 4$. Тогда количество экземпляров (30) представляет собой сумму степеней всех деревьев, которая равна $$ 30 = 4d_4 + 3d_3 + 2d_2 + 1d_1$$ но $$9 = d_4 + d_3 + d_2 + d_1$$ Устранение $d_4$ дает $$ 6 = d_3 + 2d_2 + 3d_1$$ Таким образом, общее количество деревьев степени $< 4$ не превосходит $6$, и остается не менее $3$ 4-деревьев. Следовательно, по лемме наименьшая возможная степень равна $2$, поэтому $d_1 = 0$ и $$6 = d_3 + 2d_2$$. В частности $0 \le d_2 \le 3$.

• $d_2 = 0$ дает $d_3 = 6, d_4 = 3$
• $d_2 = 1$ дает $d_3 = 4, d_4 = 4$
• $d_2 = 2$ дает $d_3 = 2, d_4 = 5$, что противоречит лемме,
• $d_2 = 3$ дает $d_3 = 0, d_4 = 6$, что противоречит лемме.

Рассмотрим случай $d_2 = 1, d_3 = 4, d_4 =4$. Обозначьте 4-деревья $A, B, C, D$, 3-деревья $1, 2, 3, 4$ и 2-дерево «$*$». Поскольку 2-дерево разделяет множества со всеми 4-деревьями $4$, эти множества должны быть $AB* := \{A, B, *\}$ и $CD*$. Не может быть набора только из 4-х деревьев, так как любой такой набор будет иметь два общих дерева с $AB*$ или $CD*$.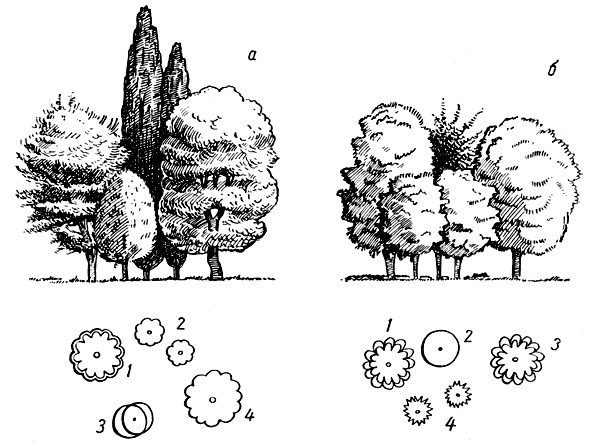 Следовательно, наборы, разделяемые парами 4-деревьев, должны иметь 3-дерево в качестве третьего члена. С помощью перемаркировки мы можем взять $AC1$ и $AD2$ как два множества. 4-й набор для $A$ должен быть $A34$, так как все остальные деревья были объединены в пары с $A$. Предположим, что $BC2$ также является множеством. Тогда $C34$ также должен быть равен $C$, поскольку он связан со всеми остальными деревьями. Это противоречит $A34$, поэтому $BC2$ не может быть множеством. Поэтому, перемаркировав при необходимости, мы можем взять $BC3$ как набор и по тем же причинам $BD4$. Остальные наборы должны быть $B12, C24, D13$, опять же, поскольку это единственные оставшиеся деревья, с которыми не были соединены 4-деревья. Это завершает список, приведенный в теореме для этого случая.

Для случая $d_3 =6, d_4 = 3$ обозначьте 4-деревья $A, B, C$ и 3-деревья $1,2,3,4,5,6$.

1. Предположим, что 4-деревья не имеют общего множества. В этом случае мы можем пометить деревья так, чтобы $AB1, AC2, BC3$ были множествами. У каждого из $A, B, C$ есть еще по два набора, которые они делят с $2$ 3-деревьями. При перемаркировке три из них — $A34, A56, B46$. Это также требует $ B25 $. $C$ остается в паре с $1, 4, 5, 6$, но $46$ и $56$ уже появились, поэтому два набора должны быть $C16$ и $C45$. Наконец, $123$ составляет последний набор.
2. Когда $ABC$ является набором, остальные наборы $9$ должны состоять из 3 наборов каждый для $A, B, C$, соответствующих им парой 3-деревьев. Это дает нам 9 вариантов пар 3-деревьев, всего ${6\choose2} = 15$, выбранных таким образом, что каждое дерево появляется в 3-х парах. Чтобы узнать, сколько существует неизоморфных вариантов, проще изучить пары $6$, которые не были выбраны. Поскольку каждое дерево встречается в 5 парах, оно должно встречаться ровно в двух оставшихся парах. Это позволяет нам формировать пути. Например, начиная с 1, выберите одно из двух деревьев в паре с ним (скажем, 3), затем возьмите другое дерево в паре с 3 (скажем, 6), затем другое дерево в паре с 6 и так далее. Поскольку всегда существует ровно одно другое парное дерево, это не может закончиться, пока вы не вернетесь к 1, образуя петлю. Каждое дерево лежит в такой петле, каждая петля имеет длину не менее $3$, а сумма длин всех петель равна $6$. Таким образом, есть только два варианта: петля длиной $6$ или $2$ петли длиной $3$. Любые две петли длины $6$ изоморфны друг другу, как и любые пары петель длины $3$. Остатки для $$ABC, A14, A25, A36, B15, B26, B34, C16, C24, C35$$ образуют $2$ петли длины $3$, а остатки для $$ABC, A14, A25, A36, B16, B24, B35, C13, C26, C45$$ образуют петлю длиной $6$. Этим исчерпываются все случаи, так что теорема доказана.

QED

Между комбинаторными решениями и геометрическими решениями нет соответствия 1-1. Действительно, оба найденных геометрических решения соответствуют $$ABC, A14, A25, A36, B15, B26, B34, C16, C24, C35$$.

Фактически,

Теорема: Не существует геометрического решения, соответствующего $$AB*, CD*, AC1, AD2, BC3, BD4, A34, B12, C24, D13$$.

Доказательство: Допустим, есть. Тогда строки, соответствующие $AB*$ и $CD*$, образуют форму V, T или X с пересечением в $*$. Предполагая, что прямые не параллельны, 3-деревья должны лежать где-то на показанных прямых. Ряды, образованные 3-деревом на прямой и 4-деревом не на ней, также должны проходить через 3-дерево на другой линии. Таким образом, расположение первого 3-дерева определяет расположение второго 3-дерева. Размещение 3-дерева из строки $AD$ в различных областях этой строки определяет регионы для 3-деревьев в строках $AC$ и $BD$, которые, в свою очередь, требуют областей для 3-дерева в $BC. $ строка. Но во всех случаях нужные области на линии $BC$ не перекрываются, что делает невозможным размещение этого дерева. Случай, когда некоторые из прямых параллельны, можно считать предельным, а значит, также несостоятельным. Для этого комбинаторного случая построить геометрическое решение невозможно.

$$\text{ V — Shape}$$ $$\begin{array}{c|cc|cc} AD & AC & DB & BC(AC) & BC(BD)\\\hline AD1 и AC2 и BD4 и BC2 и BC3\\ AD2 и AC2 и BD1 и BC2 и BC3\\ AD3 и AC3 и BD2 и BC3 и BC4\\ AD4 и AC4 и BD3 и BC1/4 и BC2\\ AD5 и AC1 и BD3 и BC1 и BC2\\ AD6, AC2, BD4, BC2 и BC3\end{array}$$

$$\text{T — Shape}$$ $$\begin{array}{c|cc|cc} AD & AC & DB & BC(AC) & BC(BD)\\\hline AD1 и AC4 и BD4 и BC1/4 и BC3\\ AD2 и AC4 и BD1 и BC1/4 и BC3\\ AD3 и AC1 и BD1 и BC1 и BC3\\ AD4 и AC2 и BD2 и BC2 и BC1/4\\ AD5 и AC3 и BD3 и BC3 и BC2\\ AD6, AC4, BD4, BC1/4 и BC3\end{массив}$$

$$\text{ X — Форма}$$ $$\begin{array}{c|cc|cc} AD & AC & DB & BC(AC) & BC(BD)\\\hline AD1 и AC2 и BD4 и BC1/4 и BC2\\ AD2 и AC2 и BD1 и BC1/4 и BC2\\ AD3 и AC3 и BD2 и BC3 и BC1/4\\ AD4 и AC4 и BD3 и BC2 и BC3\\ AD5 и AC1 и BD3 и BC2 и BC3\\ AD6 & AC2 & BD4 & BC1/4 & BC2\end{array}$$

QED

Деревья в ряд | просто пазлы

29 июля, 2016 Рекреационная математикаТеун Спаанс

Задачи на этой неделе оцениваются по 15-балльной шкале.

1. Злой лорд замка и молодой садовник
^**/*****
Давайте начнем с небольшой проблемы в этой категории, которую я разработал:
Злой лорд замка хотел поджечь красивый молодой садовник, который смотрел на свою единственную дочь. — В будущем саду уже два дерева, — сказал он отроку, — а вот еще пять. Всего получается семь деревьев. Посадите их в 6 рядов по три дерева в каждом».
Злой владыка замка вручил ему набросок, как можно посадить 7 деревьев в 6 рядов по 3 в каждом:


«Здесь есть сторожевая башня, — предупредил его владыка замка, — которую не может пересекать ни одна из трех линий. Кроме того, ни одно из двух деревьев нельзя перемещать».

Молодой садовник отправился в будущий сад и к своему огорчению обнаружил, что набросок владыки замка совершенно бесполезен, так как между двумя деревьями, стоявшими вдоль одной из сторон сада, воздвигнута тяжелая сторожевая башня:


К счастью, добрая дочь лорда замка пришла ему на помощь и предложила планировку, которая удовлетворила требованиям ее отца, оставила сторожевую башню нетронутой и не требовала перемещения двух существующих деревьев.

Вы можете проверить свои решения здесь

Обратите внимание, что задачи этого типа уже упоминались ранее:


2. * https://justpuzzles.wordpress.com/2013/02/22/10-trees-in-5-rows/
3. 9 деревьев ^***/******
   Для особо суровых придется обратиться к мастерам 19 века, он же Генри Дьюдени. Генри называет их «точечные и линейные проблемы». По словам Дьюдени, старейшая задача восходит к великому сэру Исааку Ньютону:
   Посадить 9 деревьев так, чтобы получилось 10 прямых рядов по 3 дерева в каждом.

   Вы можете проверить свои решения здесь

После сэра Исаака Ньютона Джон Джексон является следующим человеком, который ставит задачи в этой категории. В своей книге « Рациональное развлечение зимними вечерами» , опубликованном в 1821 году, Джон Джексон приводит 10 примеров таких задач. Скопирую сюда задачи, хотя решений у меня нет:

4. Джон Джексон № 1 ^***/*****
   Ваше добавление Я хочу. девять деревьев, чтобы посадить 90 101 в рядах всего пол-очка;
   и пусть в каждом ряду будет по три
   решите это: больше не прошу.
5. Джон Джексон № 2 ^***/*****
   Хотел бы я посадить рощу рядами,
   но как мне составить ее форму
   с тремя деревьями в каждом ряду
   иметь столько же рядов, сколько деревьев
   теперь скажите мне, художники, пожалуйста,
   это все, что я хочу знать.
6. Джон Джексон № 3 ^****/*****
   Изобретательные художники, пожалуйста,
   посадить рощу, молиться,
   в двадцать три ряда с пятнадцатью деревьями,
   и по три в каждом ряду
7. John Jackson № 4 ^****/******
   Требуется посадить 17 деревьев в 24 ряда
   и по 3 дерева в каждом ряду
8. Джон Джексон № 5 ^****/*****
   Гениальные художники, избавьтесь от них
   двадцать четыре дерева в двадцать четыре ряда
   три дерева я бы поставил в каждом ряду
   пруд посредине я есть также
   план этого я бы хотел
   и поэтому вам нужна помощь
9. Джон Джексон № 6 ^****/*****
   Fam’d arborists, покажите свою силу,
   и покажите, как я могу посадить беседку
   с зелеными пихтами и тисами:
   двенадцать деревьев каждого я бы избавился от
   только в двадцати восьми рядах;
   четыре дерева в каждом для просмотра.
10. John Jackson № 7 ^****/******
    Посадить 27 деревьев в 15 рядов, 5 в ряд.
11. Джон Джексон № 8 ^*****/******
    Изобретательные художники, пожалуйста,
    теперь посадите мне двадцать пять деревьев,
    в двадцать восемь рядов, ни меньше, ни более;
    В некоторых рядах пять, в некоторых три, в некоторых четыре.
12. Джон Джексон № 9 ^*****/******
    Требуется посадить 90 деревьев в 10 рядов,
    по 10 деревьев в каждом ряду; каждое дерево равноудалено
    от другого, а также каждый ряд равноудален от пруда в центре
13. John Jackson № 10 ^*****/******
    У джентльмена есть участок земли неправильной четырехугольной формы, на котором он хочет посадить пятиугольник таким образом, чтобы все ряды деревьев, будь то поперечные или диагональные, должны быть прямыми линиями. Как это должно быть сделано?

    Примечание: настоящий квинканкс — это плантация деревьев, расположенных в квадрате. состоящий из 5 деревьев, по одному на каждом углу, а пятое посередине; но в данном случае деревья должны быть расположены в виде четырехугольника, по одному в каждом углу (как в квадрате), а пятое — на пересечении двух диагоналей.

Несмотря на то, что книга с задачами легко доступна в Интернете, решения нарисованы на паре табличек, которые, увы, не прилагаются к сканам книги.
Вот подробная таблица задач Джона:

№	монет/деревьев	строк	длина строки	решение
1	9	10	3	решение
2	х	х	3	решение
3	15	23	3
4	17	24	3
5	24	24	3
6	2*12	28	4
7	27	15	5
8	25	28	3, 4 или 5
9	90	10	равноудаленных рядов
10

Дьюдени дает 5 задач в своем Развлечении по математике


14. Король и замки имел эксцентричные идеи на тему военной архитектуры. Он считал, что в симметричных формах заключена большая сила и экономия, и всегда приводил в пример пчел, которые строят свои соты в идеальных шестиугольных ячейках, чтобы доказать, что природа поддерживает его. Он решил построить в своей стране десять новых замков, которые будут соединены крепостными стенами, образующими пять линий по четыре замка в каждой. Королевский архитектор представил свой предварительный план в той форме, которую я показал. Но монарх указал, что к каждому замку можно подойти снаружи, и приказал изменить план так, чтобы как можно больше замков были свободны от нападения снаружи, и попасть в них можно было только через укрепленные стены. Архитектор ответил, что считает невозможным устроить их так, чтобы хотя бы один замок, который король намеревался использовать в качестве королевской резиденции, мог быть так защищен, но его величество вскоре просветил его, указав, как это можно сделать. Как бы вы построили десять замков и укреплений, чтобы наилучшим образом выполнить требования короля? Помните, что они должны образовывать пять прямых линий с четырьмя замками в каждой линии.
    

Вы можете проверить свои решения здесь

15. Вишня и слива ^**/*****
    

На иллюстрации изображен план коттеджа, окруженного фруктовым садом из пятидесяти пяти деревьев. Десять из этих деревьев — вишни, десять — сливы, а остальные — яблоки. Вишни посажены так, что образуют пять прямых линий, по четыре вишневых дерева в каждой. Сливовые деревья Pg 57 также посажены так, чтобы образовать пять прямых рядов по четыре сливовых дерева в каждом ряду. Задача состоит в том, чтобы показать, какие десять вишневых деревьев, а какие десять слив. Чтобы вишни и сливы имели наиболее благоприятный вид, их как можно меньше (в данных условиях) сажают на северной и восточной сторонах сада. Конечно, выбирая группу из десяти деревьев (вишня или слива, в зависимости от обстоятельств), вы игнорируете все промежуточные деревья. Другими словами, четыре дерева могут располагаться на прямой линии независимо от того, находятся ли между ними другие деревья (или дом). После последней головоломки это будет довольно легко.

Вы можете проверить свои решения здесь

16. Головоломка с плантацией ^**/*****
    

У человека была квадратная плантация из сорока девяти деревьев, но, как видно из пропусков на иллюстрации, четыре дерева были повалены ветром и удаленный. Теперь он хочет срубить все остальные, кроме десяти деревьев, которые нужно оставить так, чтобы они образовывали пять прямых рядов по четыре дерева в каждом ряду. Какие десять деревьев он должен оставить?

Вы можете проверить свои решения здесь

17. Двадцать одно дерево ^***/******
    Джентльмен хотел посадить в своем парке двадцать одно дерево так, чтобы они образовывали двенадцать прямых рядов по пять деревьев в каждом ряду. Не могли бы вы снабдить его довольно симметричным расположением, которое удовлетворяло бы этим условиям?

    Вы можете проверить свои решения здесь

18. Десять монет ^***/*****
    

Положите десять монет на большой лист бумаги или картона, как показано на рисунке, по пять с каждой стороны. Теперь уберите четыре монеты, не мешая остальные, и положите их на бумагу так, чтобы десять образовали пять прямых линий, по четыре монеты в каждой. Это само по себе несложно, но вы должны попытаться выяснить, сколькими различными способами можно решить головоломку, предполагая, что в каждом случае две начальные строки абсолютно одинаковы.

Вы можете проверить свои решения здесь

19. Двенадцать пирогов с фаршем ^**/*****
    

На нашем рисунке видно, как двенадцать пирогов с фаршем можно положить на стол так, чтобы образовалось шесть прямых рядов с четырьмя пирогами в каждый ряд. Задача состоит в том, чтобы переместить только четыре из них на новые позиции, чтобы получилось семь прямых рядов по четыре в каждом ряду. Какие четыре вы бы удалили и где бы вы их заменили?

Вы можете проверить свои решения здесь

20. Бирманская плантация ^**/*****
    Некоторое время назад я получил интересное сообщение от британского капеллана в Мейктиле, Верхняя Бирма, в котором мой корреспондент сообщил мне, что нашел на борту несколько развлечений. корабль на выходе, пытаясь решить эту маленькую задачку.

Если у него есть плантация из сорока девяти деревьев, посаженных в форме квадрата, как показано на прилагаемой иллюстрации, он желает знать, как он может срубить двадцать семь деревьев, чтобы двадцать два оставшихся сформируйте как можно больше рядов по четыре дерева в каждом ряду.

Конечно, в каждом ряду не может быть больше четырех деревьев.

Вы можете проверить свои решения здесь

21. Турки и русские ^**/*****
    Эта головоломка похожа на задачу Африди, опубликованную мной в «Tit-Bits» несколько лет назад.

    На открытом, ровном участке местности группа русской пехоты, из которой никакие две не стояли в одном и том же месте, была внезапно застигнута врасплох тридцатью двумя турками, которые открыли огонь по русским со всех сторон. Каждый из турок одновременно выпустил по пуле, и каждая пуля прошла сразу над головами трех русских солдат. Поскольку каждая из этих пуль при выстреле убила другого человека, задача состоит в том, чтобы выяснить, каково наименьшее возможное количество солдат, из которых могла состоять русская сторона, и каковы были потери с каждой стороны.

    No related posts.